本文是POPL2022同名文章的中文翻译,無断転載禁止。
关于match types的Scala文档:https://docs.scala-lang.org/scala3/reference/new-types/match-types.html
Type-level programming在FP越来越流行,但type-level programming和subtyping的组合还没有充分的探索。这篇文章中的match types等价于类型层面的pattern matching,在基于system F$_{<:}$的一个演算上形式化了match type这个feature,证明了它的soundness。在Scala3的reference compiler上实现了match types的系统。
1. Introduction
原本只属于依值类型语言的特性开始飞入寻常百姓家,使用类型层面计算以增加类型系统的表达能力,表达类型层面上更多的constraints,提高软件的安全性。GHC Haskell一直是这个过程的前沿,并且已经提高了许多extension以支持type-level programming。虽然Haskell也不是唯一一个,但是这个潮流似乎局限于纯FPL。
事实上,Haskell语言是不支持dependent type的。
GHC Haskell中主要提供type-level programming功能的是type families和data kinds这两个拓展。type family提供了类型上的计算(类型上的pattern matching),data kinds提供了在type level定义data的能力(将value提升到type level的能力),可以实现一定的dependent type。
我们认为type-level programming并不一定与其他编程范式不相容,当下的分裂格局主要源于学界的对这一领域的不重视。不幸的是,这个领域现有的研究都不能直接应用于有subtyping的语言。尽管subtyping和type-level programming结合在理论界通过依值类型系统被广泛研究,但在实践层面还有很多没有探索。
Haskell所使用的Hindley-Milner类型系统与subtyping是不兼容的。
一个例外是TypeScript,最近引入了一个叫conditional type的特性,一个基于subtyping的类型层面三目运算符。S extends T ? Tt : Tf在S是T的子类型时归约到Tt,在S不是T子类型时归约到Tf,否则如果无法给出结论,就不做归约。遗憾的是,归约这个conditional type的算法是既unsound又incomplete的。尽管它不sound(见6.5),TypeScript这个新特性的添加还是展现了这个需求的存在。
这篇文章展示了基于subtyping的type-level programming的另一种构造,称为match types。顾名思义,match types允许用户使用类型上的pattern matching来表达类型:
1 | type Elem[X] = X match { |
将在第2节中解释这个例子,它定义了一个Elem类型,匹配类型参数X。我们已经在最新版本的Scala3(一个工业级的编译器)上实现了match types,已经获得了Scala社区的很大兴趣,并投入活跃使用。
这篇论文中,通过一个可以在System F$_{<:}$上扩展了项和类型层面的pattern matching的一个类型系统的lens,我们探索了match types的理论基础。我们的形式化有两个目的:一、展示如何在Scala的类型系统中整合match types,并精确的描述在子类型关系上还需要作出的改变以确保这个整合的可能性。二、得益于标准的progress和perserve定理的类型安全证明,给了我们信心match types的设计是合理的并且它的实现是sound的。
Conditional types提供了确凿的证据表明我们的成果在Scala之外也是有价值的。我们的成果可以直接应用于Typescript的类型系统,并提供能修复引入conditional types带来的unsoundness的一个清晰的路线。进一步,我们希望match types可以为未来的有subtyping的语言的type-level programming特性的设计作为一个参考。
总结,这篇论文做了以下工作:
通过一个例子介绍在Scala中的match types编程,并突出了它与type-level programming和subtyping的关系(2)
我们在self-contained calculus System FM中形式化了match types,并证明了它sound,提供了我们的理论基础的实现(3)
描述了我们实现的Scala编译器中的match types,讨论了挑战,以及这个实现和我们的形式化之间的联系(4)
通过一个案例分析评估了match types,呈现了Numpy库的一个类型安全版本(5)
我们的形式化的设计与先前的相关工作,重新审视了相关的Haskell中type families的大量工作,并讨论了Typescript中的conditional types的unsoundness(6)
2. Overview
这一节中,我们通过上文的一个例子,提供一个Scala中的match types的简要介绍:
1 | type Elem[X] = X match { |
这个例子定义了一个类型Elem,关于一个类型参数X。等号右边是通过一个在类型参数上的match定义的,一个match type。一个match type归约到右边的其中的一个,取决于它scrutinee的类型。例如,上面的类型归约到如下:
没看到过scrutinee这个术语,下文解释了,见3.2,大概是被match的对象的意思。
1 | Elem[String] =:= Char |
此处S =:= T表记类型S和T的相等性,定义为互为子类型。要归约一个match type,scrutinee与每个pattern通过subtyping关系一一比较。例如,尽管String既是String又是Any(Scala子类型格的top)的子类型,Elem[String]归约到Char因为它对应的case先出现。
当scrutinee类型是个List,match type Elem是在这个列表中的元素类型上的递归定义。因此,在这个例子中的Elem[List[Int]]首先归约到Elem[Int],然后最后归约到Int。
2.1 依值类型的一个轻量级形式
Match types可以提供一个轻量级形式的依值类型,因为一个term-level的pattern matching表达式可以在类型层面作为match type对应的被定型。考虑下面的函数定义:
1 | def elem[X](x: X): Elem[X] = x match { |
这个参数化类型X与Haskell中的forall类型的语义不同,Haskell中forall修饰的类型参数无法对类型的性质做假设,或者pattern matching之类的操作。例如,具有
forall a . a -> a签名的函数只有id一个。
这个定义是良类型的,因为在elem体中的match表达式有和Elem[x](函数的返回值类型)完全相同的scrutinee和pattern类型。
归功于Scala的类型推断,elem函数的一个调用得到一个返回值类型,依赖于一个term-level的参数。例如,表达式elem(1),Scala编译器会给elem的类型参数推断出一个singleton type X = 1,于是这个表达式的类型是Elem[1],(根据Elem的第三个pattern)归约到Int。类似的,在elem(x)中,编译器推断singleton type X = x.type,则这个表达式有类型Elem[x.type],这可能会根据调用时x的类型进一步归约。
关于singleton type:
- https://docs.scala-lang.org/sips/42.type.html#inner-main
- https://stackoverflow.com/questions/33052086/what-is-a-singleton-type-exactly
我感觉singleton type和GHC Haskell的DataKinds挺像的,是指每一个(字面量)值都有一个对应的singleton type,建立了值与类型之间的桥梁,也提供了dependent type的一个侧面。
此处,
elem(1)会给字面量1一个最紧的类型1 : 1(考虑子类型关系下,最松的是Any,就等于啥都没推断了)。
在这两个例子中,singleton types创造了一个类型参数和一个项之间的依赖,由传递性,可以得到一个轻量级的依值类型,即项参数和函数返回类型的依赖关系。
2.2 不相交性
我们设计的match types在归约时会归纳一个额外的限制:scrutinee类型必须要与所有的case的类型不相交。非形式化的说,不相交就是两个类型没有相同的居留元。
举例介绍这个不相交性的重要性。考虑整数序列的类型Seq[Int],则Elem[Seq[Int]]不会被归约:
- 第一个case无法应用,因为
Seq[Int]不是String的子类型 - 第二个case无法应用,因为
Seq[Int]不是List[Int]的子类型(反过来倒是成立) - 第三个case不作考虑,因为
Seq[Int]与List[Int]并不具有不相交性。
因此,归约算法会在第二个case卡住,于是整个type都不可归约。如果没有不相交性,那么Elem[Seq[Int]]会被归约到Seq[Int](根据第三个case)。这是unsound的。因为例如表达式elem[Seq[Int]](List(1,2,3))会有类型Seq[Int],但求值出来是整数1。
这里还是没太懂这个case3是怎么来的。先往下看看rule吧
3. Formalization
在这一节里,我们会形式化的描述System FM,这是System F<:的一个对pattern matching、opaque class和match types的拓展。图1定义了FM的语法和求值关系。图2定义了FM的类型系统,包括三个关系:定型、子类型和类型不相交性。在3.1和3.2中讨论了与System F$_{<:}$ 的区别。在3.3中提供了一个System FM的type safety的证明的提纲。在3.4中我们介绍一个System FM对在类型pattern中绑定pattern变量的支持的拓展。
opaque class是啥?


3.1 类
System FM是由一个带类继承$\Psi$的类的集合$\text{C}$,和类的不相交性$\Xi$为参数的。其中,类继承是$\text{C}$上一个偏序关系,即自反、反对称和传递的。而类的不相交性是$\text{C}$上的一个对称关系。类之间的子类型是通过$\text{S-PSI}$规则由$\Psi$决定的。
继承和不相交性这两个参数可以理解为Scala中trait和类的架构的一种表示。比如,trait C1; class C2 extends C1在FM中被表示为$\Psi=\lbrace (\text{C}_1,\text{C}_2)\rbrace ;\ \Xi=\lbrace \rbrace $。这样的表示同时也建模了哪些类型不能有相同的实例。例如,class C3; class C4表示为$\Psi=\lbrace \rbrace ;\ \Xi=\lbrace (\text{C}_3,\text{C}_4),(\text{C}_4,\text{C}_3)\rbrace $,因为Scala不允许多继承。继承和不相交性必须具有一种一致性:$(\text{A},\text{B})\in \Xi$蕴含着不存在类$\text{C}$使得$(\text{C},\text{A})\in \Psi$且$(\text{C},\text{B})\in \Psi$。
来自梁老师的勘误,局的应该是$\Psi=\lbrace (\text{C}_2,\text{C}_1)\rbrace $,C2是C1的子类
即如果A和B不相交,则不存在一个C类,使得C同时是A和B的子类,因为否则的话C的实例就同时是A和B的居留元了。
$\text{C}$中的每个类有一个构造子(记作$\textit{new }\text{C}$),一个类型(记作$\text{C}$),和一个singleton type构造子(记作$\lbrace \textit{new }\text{C}\rbrace $)。类型$\text{C}$表示所有继承$\text{C}$ 的值,而singleton type构造子表示一个单个的值:即$\text{C}$构造子的调用。
就是说类型C的居留元包括所有C或者C的子类型的构造子的调用,而C的singleton type的居留元只包括C构造子的调用。
这样参数化的实现方式使我们可以对OO语言中的类继承架构建模,而不需要专门的类和数据类型定义的语法。尽管我们的方式可能过于简化,但它可以轻松地建模如多继承等高级OO特性。我们将在4.1节讨论把Scala的类型编码进System FM。
我们的类型系统是通过名字来引用这些类,所以会混淆结构上的(structural)和名义上的(nominal)类型。名字可以有效地提供一个运行时的标签(tag)和编译期的类型之间的一个直接的对应。我们之后会发现,运行时的tag已经足够进行运行时的类型测试,而且在pattern matching的求值过程中也起到了核心的作用。
3.2 Matches
System FM同时支持term-level(match expressions)和term-level(match types)的pattern matching。不管是哪种Match,都由一个scrutinee,一个case的列表,和一个缺省表达式/类型组成。每个case由一个type test和一个对应的表达式/类型组成。在term level,type test是由一个对一个特定类的继承(关系)检查(也被称为typecase)组成的。在type level,type test对应着一个特定类型的子类型(关系)检查。这个区别反映了运行时(type test是通过类表实现的)和编译期(在类型系统的限度里比较类型)。我们将在4.6节讨论在运行时的Scala类型。
见图1的语法:
term level的match:$\text{t }match\lbrace \overline{\text{x:C}\Rightarrow\text{t}}\rbrace or\ \text{t}$
type level的match:$\text{T }match\lbrace \overline{\text{T}\Rightarrow\text{T}}\rbrace or\ \text{T}$
scrutinee应该就是对应的match前的t和T。
在term level,type test(也就是type system要对这个match做的工作)是检查scrutinee与$\text{x:C}$,也就是那个t是否是C的一个子类型的居留元(就像动态指派一样)
而在type level,type test是检查那个T是否是$\Rightarrow$前的T的子类型(这理论上是个静态的事情)
正如最后一句所说。
在这个文章中,我们使用简短的语法$t_s\ match\lbrace x_i:\text{C}_i\Rightarrow t_i\rbrace or\ t_d$表示一个任意数量的case,即$\exists n\in\mathbb{N}.\ t_s\ match\lbrace x_1:\text{C}_1\Rightarrow t_1;\dots;x_n:\text{C}_n\Rightarrow t_n\rbrace or\ t_d$。
Match expression和match type由$\text{T-MATCH}$定型规则相关联。这个规则对一个match expression的每个组成部分做定型,然后整合对应的match type。
Example A. 例如,给定两个不相交的类A和B,和一个空的类继承架构($\Psi=\text{Id},\ \Xi =\lbrace (\text{A},\text{B}),(\text{B},\text{A})\rbrace $),则下面的函数
$$
\text{f}=\lambda \text{X<: Top.}\ \lambda\text{x:X.x }match{\text{a:A}\Rightarrow \text{foo;b:B}\Rightarrow \text{bar}}or\text{ buzz}
$$
可以被精确地定型为:
$$
\text{f}\ :\ \forall\text{X<:Top. X}\to\text{X }match{\text{A}\Rightarrow\text{Foo;B}\Rightarrow\text{Bar}}or\text{ Buzz}
$$
subtyping格的Top就是Any类型,即X可以是任意类型。
$\lambda$表示term-level的抽象,$\Pi/\forall$表示type-level的抽象。
定型的结果是将term-level的match变成了type-level。
其中foo,bar和buzz分别是类型为Foo,Bar和Buzz的表达式。
match expression的cases是顺序求值的:scrutinee通过对每个case的type test一个接一个进行检查。整个表达式归约到第一个type test成功的对应表达式($\text{E-MATCH2}$)。当没有成功的type test时,则归约到缺省的表达式($\text{E-MATCH3/4/5}$)。例如,A中定义的函数f,表达式$(\text{f A }(\textit{new }\text{A}))$求值到foo,而$(\text{f B }(\textit{new }\text{B}))$求值到bar。
Match Type Reduction 为了实现match type的归约,子类型关系包括5个规则:$\text{MATCH1/2/3/4/5}$。这些规则是用$=:=$的对表记的,其中$\text{S}=:=\text{T}$表示S和T互为子类型。更准确地说,图2中的$\text{S-MATCH1/2}$对应着两个有着相同的前提和对称的结论的typing rules,$\text{S-MATCH}3/4$也同理。
通常来说我们好像觉得是先有相等关系再由偏序关系的三个性质,但仔细想想好像不是的。所谓的相等关系就是等价关系,也就是集合上的一个划分。偏序关系和等价关系不一定哪个更本质。
从子类型的语义上来说,子类型关系是一个在类型上的偏序关系。从它的subtyping rule中我们可以看到$<:$的自反和传递性都是公理。
而反对称性是建立在一个对应的等价关系上的。要知道这个类型系统的$<:$是否满足反对称性,就要知道$A<:B\ \wedge\ B<:A$是不是一个等价关系。这个可能就是这个类型系统需要保证的(需要证明的一个性质)。
而在证明了它是个等价关系之后,这个类型系统把$A<:B\ \wedge\ B<:A$记作了$A=:=B$,这就定义了这个类型系统上的一个相等性。
$=:=$是一种meta的表记,用$<:$写的话就是4条rule,从定义上说$<:$更本质。
这也是为什么在System F上没有定义类型的相等(或者说类型上的相等性就是identical)。
match type归约的typing rule的最好解释是一个求值关系的推广。给定一个match type,$\text{M=T}_s\ match\lbrace \text{C}_i\Rightarrow \text{T}_i\rbrace or\ \text{T}_d$,M归约到$\text{T}_i$,当且仅当对于$\text{T}_s$中的每个值$\text{t}_s$,term level的表达式$\text{t}_s\ match\lbrace \text{x}_i:\text{C}_i\Rightarrow \text{t}_i\rbrace \ or\ \text{t}_d$求值到$\text{t}_i$。
$\text{S-MATCH1/2}$规则对应着一个match expression求值到它的第n个case($\text{E-MATCH2}$):
$$
\dfrac{\Gamma\vdash\text{T}_s<:\text{S}_n\quad \forall m < n.\Gamma\vdash \text{disj}(\text{T}_s,\text{S}_m)}{\Gamma\vdash\text{T}_s\ match{\text{S}_i\Rightarrow\text{T}_i}or\ \text{T}_d=:=\text{T}_n}\quad(\text{S-MATCH1/2})
$$
第一个前提确保了第n个case的type test会对所有的有$\text{T}_s$这个scrutinee type的值都成功。反之,第二个前提是一个不相交的判定,保证了有scrutinee type的value没有一个能通过在第n个case之前的type test。$\text{S-MATCH3/4}$规则对应着求值到缺省case($\text{E-MATCH2}$),需要scrutinee type和每个type test类型之间不相交:
$$
\dfrac{\forall n.\Gamma\vdash\text{disj}(\text{T}_s,\text{S}_n)}{\Gamma\vdash\text{T}_s\ match{\text{S}_i\Rightarrow\text{T}_i}or\ \text{T}_d=:=\text{T}_d}\quad(\text{S-MATCH3/4})
$$
两个类之间的不相交性可以直接由使用了类不相交性$\Xi$的$\text{D-XI}$规则得到。另外,一个构造子singleton type和一个类之间的不相交性可以直接观察类继承关系$ \Psi$得到($\text{D-PSI}$)。函数类型和universal类型与类不相交,因为他们居留着不同的值($\text{D-ARROW,D-ALL}$),所以他们也永远不会匹配。最后是不相交性规则,$\text{D-SUB}$,说明了如果U和T不相交,那么所有U的子类型也和T不相交。
Example B. 我们继续看Example A,展示怎么使用match type的归约规则来推出$(\text{f B (}new\text{ B)})$的类型是Bar。使用$\text{T-TAPP, T-APP}$,表达式可以被定型为:
$$
\text{f B (}new \text{ B)}\ :\ \text{B }match{\text{A}\Rightarrow\text{Foo};\text{B}\Rightarrow\text{Bar}}or\text{ Buzz}
$$
因为我们的例子假设了一个空的类继承关系,并且$\text{(A,B)}\in\Xi$,所以$\text{S-MATCH1}$规则得到:
$$
\emptyset\vdash\text{B}\ match{\text{A}\Rightarrow\text{Foo};\text{B}\Rightarrow\text{Bar}}or\ \text{Buzz<:Bar}
$$
最后,使用$\text{T-SUB}$规则,我们得到$\text{(f B(}new\text{ B)):Bar}$。
子类型和不相交性。有人可能有疑问如果我们把match type的归约规则简化一下,把前提$\Gamma\vdash\text{disj(T,C)}$换成看似等价的前提$\text{(T,C)}\notin\Psi$会怎么样。遗憾的,这样的话这个系统就会unsound了,举反例说明。假设Example A里面定义的函数f,加一个新的类E并且$\Psi=\lbrace \text{(E,A),(E,B)}\rbrace ,\Xi=\lbrace \rbrace $。现在考虑项$\text{(f B(}new\text{ E))}$。因为有$\emptyset\vdash\text{E<:B}$, 这个函数应用是良类型的,并且由于$\text{(E,A)}\in\Psi$,会求值到foo。这样,term-level和type-level的归约就不一致了!当对更改后的$\text{S-MATCH1}$规则用$\text{(B,A)}\notin\Psi$,就会得到错误的结论$\text{(f B (}new\text{ E))}$有Bar的错误结论,导致了unsoundness。这会导致类型$\text{e : Bar}$和求值$\text{(e}\to\text{foo)}$之间的不一致,就破坏了类型系统的soundness。在System FM中,对$\text{(f B (}new\text{ E))}$定型得到的match type并不会归约,因为scrutinee type B与test A的第一个pattern type既不是不相交的,也不是子类型。在这个情况下,没有归约的match type会被赋值为”as is”(原样)。没有归约的类型的出现可以是一个程序错误,但也可以是因为一个match type的局部不可归约。例如,Example A中的f被定型为一个未归约的类型,但这个类型之后可以依赖于类型变量的实例化而被归约。
3.3 类型安全
我们通过通常的progress和preservation定理来展示System FM的类型安全。这一节提供了一个证明架构的概览并且描述了包括的引理和定理。详细的纸面证明详见这个文章的附录。也提供的Coq的机器证明。我们的机器证明使用的局部匿名的表示来对变量绑定做建模,并且简化了match type的表示使得每个match有且只有一个case。多个case的match可以通过嵌套在default case里来表示。
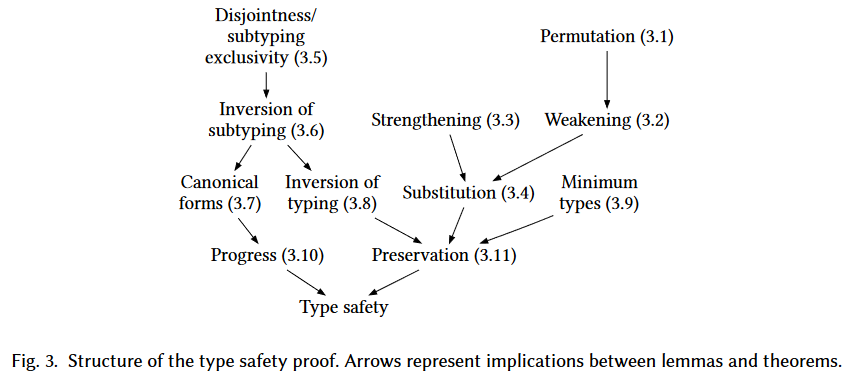
图3给出了一个证明架构的概览,展示了引理和定理之间的蕴含关系。基本的结构和System F$_{<:}$的标准证明类似。接下来介绍我们的类型安全证明里面的引理和定理。
Preliminary Lemmas。我们的证明从初等的引理开始:LEMMA3.1(PERMUTATION,排列引理),LEMMA3.2(WEAKENING,弱化引理),LEMMA3.3(STRENGTHENING,强化引理),LEMMA3.4(SUBSTITUTION,置换引理)。我们省略了这些引理,因为它们是完全标准的,但相对冗长,因为它们跨越了我们系统的三种关系:定型、子类型和不相交性。像往常一样,他们的证明遵循推导的相互归纳。(?
Disjointness / Subtyping的互斥性(Exclusivity)。接下来的非标准的引理可以防止$\text{S-MATCH1/2}$和$\text{S-MATCH3/4}$之间的存在交集的可能。
- LEMMA3.5 (Disjointness/subtyping exclusivity) 类型的不相交性和子类型关系是互斥的
如果允许存在这种重叠,match types就可以有多种归约方式,系统就unsound了。我们用反证法证明了Lemma3.5。我们的证明把SystemFM的类型映射到一个新定义的集合$\text{P}=\lbrace \Lambda,\text{V}\rbrace \cup\text{C}$的一个非空子集中。$\text{P}$可以理解为一个FM类型上的等价类。我们展示了在FM中的子类型关系对应着$\text{P}$中的一个子集关系,而FM类型的不相交关系是$\text{P}$中的集合不相交关系。这个集合论的视角可以直接得出我们需要的结论。在我们的Coq实现中,我们直接把这个引理设为公理了,证明交给了纸面证明。
子类型的逆 Inversion of Subtyping。接下来的Lemma3.6使我们能够实现子类型关系上的逆,这个对canonical form(Lemma3.7)和typing的逆(Lemma3.8)很重要。这个引理的陈述需要定义一个新的关系,记作$\Gamma\vdash\text{S}\rightleftharpoons \text{T}$,见图4的定义。它表述了存在一个证明,使得match type $\text{S}$和类型$\text{T}$互为子类型,并且满足一个额外的条件:这个证明过程是$\text{S-MATCH1/2}$,$\text{S-MATCH3/4}$和$\text{S-TRANS}$在两个方向上成对使用的。直观来说,$\Gamma\vdash S\rightleftharpoons T$比$\Gamma\vdash\text{S<:T}$和$\Gamma\vdash\text{T<:S}$这两个独立的证明派生要更好用,因为它允许两个subtyping方向的simultaneous induction(?)
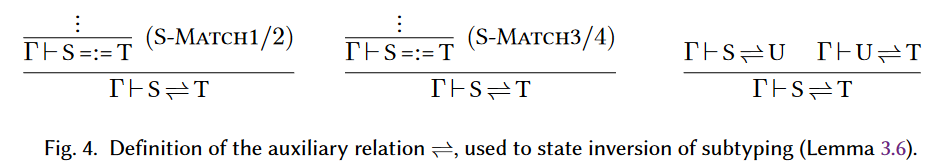
这里把1/2和3/4的$=:=$这个meta表记还原一下:
$$
\dfrac{\dfrac{\vdots}{\Gamma\vdash\text{S<:T}}(\text{S-MATCH1})\quad\dfrac{\vdots}{\Gamma\vdash\text{T<:S}}\text{(S-MATCH2)}}
{\Gamma\vdash\text{S}\rightleftharpoons \text{T}}\
\dfrac{\dfrac{\vdots}{\Gamma\vdash\text{S<:T}}(\text{S-MATCH3})\quad\dfrac{\vdots}{\Gamma\vdash\text{T<:S}}\text{(S-MATCH4)}}
{\Gamma\vdash\text{S}\rightleftharpoons \text{T}}
$$
就可以理解啥是“成对使用”了。那么为啥要成对使用呢?
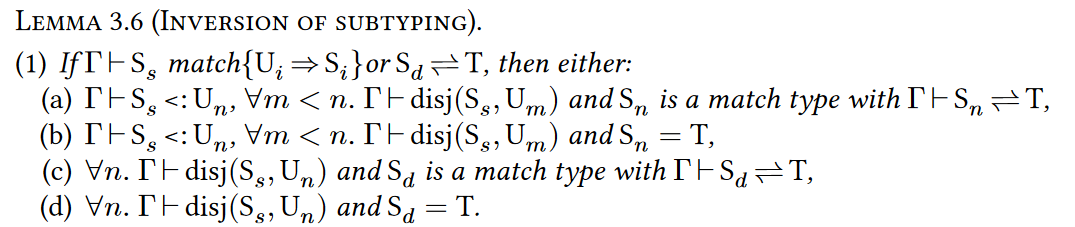
如果$\Gamma$下可以定型左边这个match type和T是互为子类型的,那么下面有一个成立
(a) $\text{S}_s$是第n个pattern的子类型,并且对于所有n之前的pattern都和$\text{S}_s$都不相交,并且第n个pattern对应那个$\text{S}_n$(也是一个match type)然后也能定型为和T是互为子类型(大概就是归纳)
(b) $\text{S}_s$是第n个pattern的子类型,并且对于所有n之前的pattern都和$\text{S}_s$都不相交,并且第n个pattern对应那个$\text{S}_n$就是T(这个等号没有定义,我怀疑就是指identical,这个大概是base case)
(c) $\text{S}_s$和所有的pattern都不相交(那么就归约到缺省),并且$\text{S}_d$(也是一个match type)然后也能定型为和T是互为子类型(大概就是归纳)
(d) $\text{S}_s$和所有的pattern都不相交(那么就归约到缺省),并且$\text{S}_d$就是T(这个大概是base case)
这个大概意思是一个类型T和一个match type如果互为子类型,那么有的性质(分类讨论)
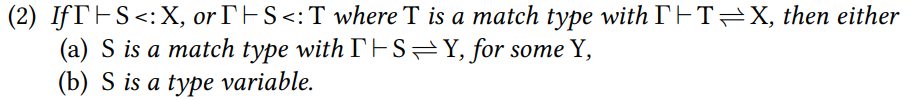
如果$\Gamma$下可以定型S是X的子类型,或者S是T的子类型,其中T是一个match type然后T和X是互为子类型的,那么
(a) 要么S是一个match type然后存在某个Y和它互为子类型
(b) 要么S是一个类型变量
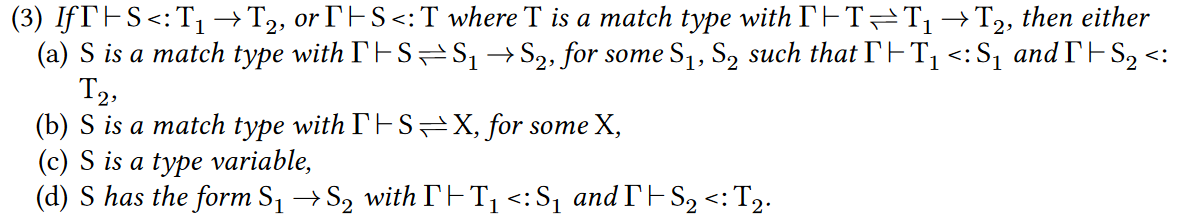
如果$\Gamma$下可以定型S是$T_1\to T_2$的子类型,或者S是T的子类型,其中T和$T_1\to T_2$是互为子类型的,那么下面有一个成立
(a) S是一个match type,存在S1S2,S和$S_1\to S_2$互为子类型,使得T1是S1的子类型,S2是T2的子类型
(b) S是一个match type,存在X,使得S和X互为子类型
(c) S是个类型变量
(d) S形如$S_1\to S_2$,T1是S1的子类型,S2是T2的子类型
这条处理函数类型
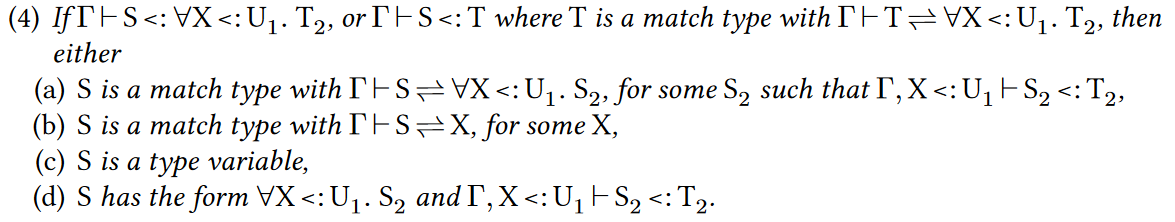
如果$\Gamma$下可以定型S是$\forall X<:U_1.T_2$的子类型,或者S是T的子类型,其中T是一个match type,T和这个全称量化类型互为子类型,那么下面有一个成立
(a) S是一个match type,,,
这条处理全称量化类型
Lemma3.6的第一条使用了$\rightleftharpoons$的结构提供了一种逆,我们用它来证明后续的几点。对比$\text{F}_{<:}$类型安全证明中相应的inversion lemma,Lemma3.6的陈述和证明要更长更复杂。这个区别是不可避免的,因为match type的归约规则允许match expression作为归约的结果,使这个inversion变得复杂了。
类似于Subtyping的inversion,我们的canonical forms lemma是非标准的,因为它使用了它的前提的一个析取来解释match types。
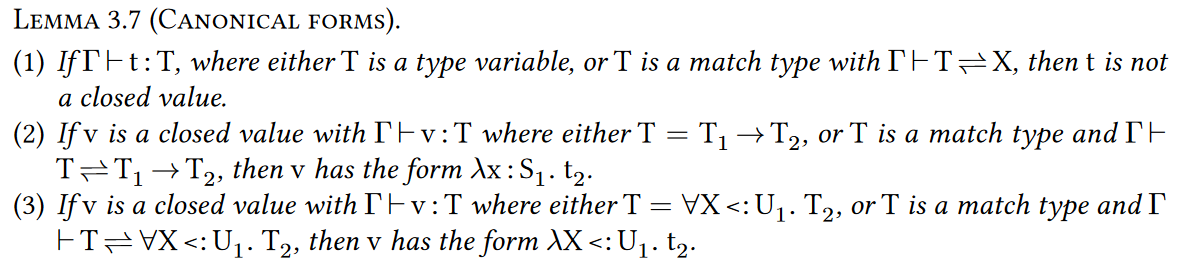
- 如果$\Gamma$下可以定型t是T类型,其中T要么是个类型变量,要么是一个match type然后T和某个类型X互为子类型,那么t不是一个closed value
- 如果v是一个closed value,定型为要么是$T_1\to T_2$,要么是一个和$T_1\to T2$互为子类型的类型,那么v一定形如$\lambda x:S_1.t_2$
- 如果v是一个closed value,定型为要么是$\forall X<:U_1.T_1$,要么是一个和他是互为子类型的类型,那么v一定形如$\lambda X<:U_1.t2$
value是特殊的term,closed value就是既close又value的term。
Soundness的证明。剩下的soundness的证明基本上是标准的。Lemma3.8和3.9是简单的typing rule的逆。在preservation的证明中需要Lemma3.9去从typing judgments中恢复subtyping的界。证明是通过derivation上的routine induction完成的。
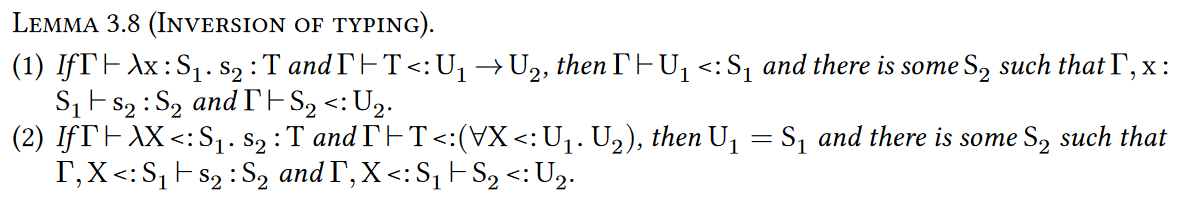
- 如果$\Gamma$下可以定型$\lambda x:\text{S}_1.\text{s}_2$类型是T并且T是$U_1\to U_2$的子类型,那么U1是S1的子类型并且存在S2使得$\Gamma,x:S_1\vdash s_2:S_2$且S2是U2的子类型
- 如果$\Gamma$下可以定型$\lambda X<:S_1.s_2:T$,并且T是$\forall X<:U_1.U_2$的子类型,那么U1就是S1,并且存在S2使得$\Gamma,X<:S_1\vdash s_2:S_2$并且$\Gamma,X<:S_1\vdash S_2<:U_2$
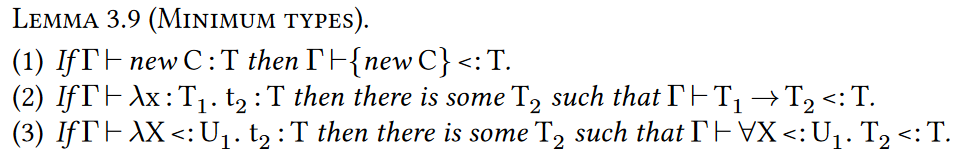
- 如果$\Gamma$下能定型new C是T类型,那么单例$\lbrace new C\rbrace $是T的子类型
- 如果$\Gamma$下能定型$\lambda x:T_1.t_2$是T类型,那么存在T2使得$T_1\to T_2$是T的子类型
- 如果$\Gamma$下能定型$\lambda X<:U_1.t_2$是T类型,那么存在T2使得$\forall X<:U_1.T_2$是T的子类型
有了这些引理,就可以直接得到progress和preservation了。
懂的都懂
3.4 类型绑定扩展
这一节,我们展示System FMB,是System FM拓展了在type pattern中绑定pattern variables的支持。FMB由两个参数组成,是两个类的集合A和B,分别表示非参数化和参数化的类。一个参数化的类,写作B T,恰好接受一个类型参数。我们精化C成为一个语法上的对象,定义为$C::=A|B\ T$。类继承关系$\Psi$和类不相交关系$\Xi$还是C上的二元关系不变。类继承架构上的一个泛型的实例化用$\Psi$中的一个元素表示,例如,A1 extends B2[A3]表示为$(A_1,B_2,A_3)\in \Psi$。泛型的继承用$\Psi$中的多个元素表示,例如,B1[T] extends B2[T]表示为$\forall T.(B_1\ T, B_2\ T)\in \Psi$。这个做法让我们可以复用FM中的大部分定义。确实,我们的形式化把C,$\Psi$和$\Xi$作为数学对象处理,然后这与FMB中的类的新定义是兼容的。
原文注:这个限制一个类型参数是为了表示上的目的。System FMB的类型系统和类型安全的证明都可以轻松地运用到一个可以支持多个参数的绑定变量。
在图5中,我们定义了System FMB的语法和规则,其中灰色的是较FM的改动。FMB对于match expression和match types的新语法在构造中增加了一个pattern variable。在$\text{t}_s\ match[X]\lbrace \text{x}_i:\text{C}_i\Rightarrow\text{t}_i\rbrace or\ \text{t}_d$中,pattern变量X现在可以在Ci pattern中绑定类型参数了。

$\text{S-MATCH3/4}$,$\text{S-MATCH5}$和$\text{T-MATCH}$需要很小的改动就可以在定型上下文中使用pattern variable了。注意到pattern variable是无条件出现在上下文中的,不论这些变量是否在对应的pattern中被使用了。
在新的子类型规则中,对于非缺省的match归约,$\text{BS-MATCH1/2}$,第一个前提实例化了pattern变量X到某一个类型U使得那个scrutinee类型是第n个pattern的一个子类型。
这里的U是完全不受约束的:任何X的实例,使得Ts是Sn的子类型的都是可以的。不相交性的judgment对于X,比起subtyping judgment(X<:Top而不是X<:U)使用了一个更弱的上界,这是因为scrutinee类型必须要和没匹配上的pattern类型对于X的所有可能的实例都不相交。在算法的系统中,U会在类型推断的时候通过约束的求解被计算出来。
对于非缺省match归约的新的求值规则($\text{BE-MATCH2}$)使用了一个类似的机制:它先找第一个case使得可以实例化这个pattern variable让那个scrutinee继承自那个对应的pattern
第二个前提排除了一个全称量词覆盖了整个类型的不匹配的情况。一个具体的实现肯定会选择一个更高效的方式,比如把$\Psi$实现为一个lookup table。
Exmaple C。考虑下面的类继承结构,有两个类Char和String,和一个单类型变量的类List,使得String继承了List Char:
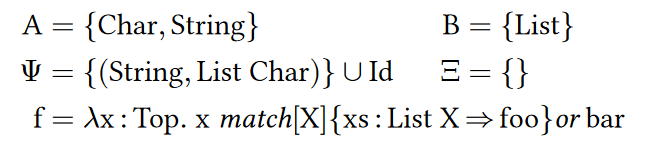
这个f匹配了他的参数到List X这个pattern,其中X是个pattern variable。我们通过两个应用检查这个evaluation:
- $\text{f}(new\ \text{String})$,匹配List X的话X=Char,会通过$\text{BE-MATCH2}$(因为$(\text{String,List Char})\in\Psi$)求值到$[\text{X}\mapsto \text{Char}][x\mapsto new \text{ String}]\text{foo}$。
- $\text{f}(new\ \text{List Top})$,也匹配List X,这次X=Top,然后通过$\text{BE-MATCH2}$求值到$[\text{X}\mapsto \text{Top}][x\mapsto new \text{ List Top}]\text{foo}$。这里$(\text{List Top, List Top})\in\Psi$是从$\Psi$的自反性得到的。
我们通过使用System FM的纸面证明建立了System FMB的类型安全。需要做的改动很冗长,相对无趣,就是在context里维护一个额外的pattern variable。FMB 类型安全的主要内容是证明不需要对 BS-Match1/2 中的类型 U 进行额外的约束。因此,算法实现可以自由地使用任何机制来提出模式变量的实例化。
4. 实现
Match types在Scala的参考编译器Dotty上实现了。这段解释了我们怎么把实现和3里面的形式化关联起来的。
就像System FM中的一样,在编译器中,match-type归约在子类型定型时出现。为了让子类型定型保持为一个算法,match type的归约规则从来不能引入新的match type,只能化简原来的程序。归约算法与第3段中的定型规则紧密的结合。scrutinee类型与每个pattern顺序地作比较。如果scrutinee类型是第一个pattern类型的子类型,那么归约。否则,如果scrutinee类型可以知道和第一个pattern类型不相交,那么这个算法会到下一个pattern,如果算法到了一个既不是子类型,又可以确定不是不相交的类型,那么就终止归约,留下原来的match type。
4.1 Scala中的不相交性
分离编译是两个判断两个类型不相交的最大障碍。确实,在Scala中,所有的traits和类都是自动可以被继承的。因为Scala的程序是在一个开放世界假设下编译的,类型经常会是在当前的编译单元是不相交的,但在未来的某次编译中,为了潜在的扩展,编译器必须做保守估计。
分离编译就是为什么我们的形式化需要两个参数来表述类继承架构的原因。System FM的一个特定的实例化可以被理解为Scala类型系统对于某一特定编译单元的一个模型,其中C表示目前已经定义的类。类继承关系$\Psi$,对于所有子编译单元有效:新的定义不会改变之前定义的继承关系。然而,类继承关系$ \Psi $自己并不足以得到两个类的不相交性:新的类定义可能引入两个已经存在的类的交集。因此,我们的形式化使用了一个分开的参数($ \Xi $)去描述类的不相交关系。对于分离编译,$\Xi$应该只包含那些即使考虑了潜在的对于类集合的扩充也仍然保持不相交的类的对。
感谢Scala提供了多种途径限制可扩展性。trait和类上的sealed和final表记直接限制了标注类型的可扩展性:sealed类型只能声明的在同一个文件里被扩展,于是提供了一个枚举所有子类的途径。因此,sealed trait和类的的不相交性可以通过遍历这个类型的每个可能的子类型来递归地计算。trait和类的主要区别是类最多只能继承一个父类。这个性质使编译器可以通过一个简单的检查断言两个类的不相交性:给定两个类A和B,如果A不是B的子类型,B也不是A的子类型,那么没有类可以同时继承这两者,所以他们就是不相交的。
作为一个例子,考虑下面的Scala定义(左边)和对应的System FM的实例化(右边):
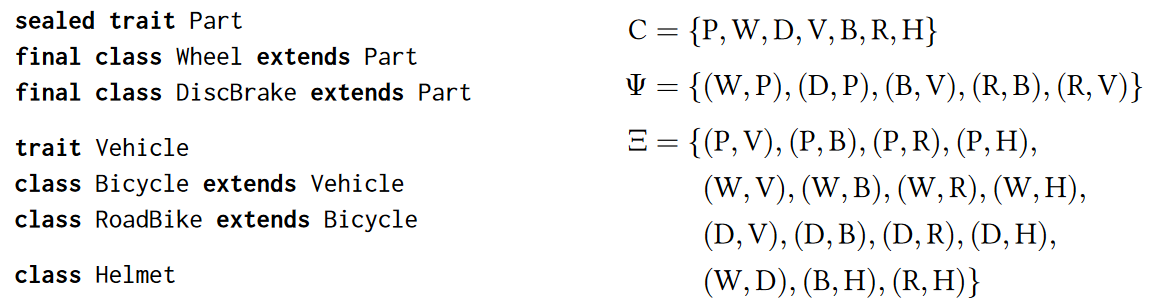
类和继承关系在两种表示中几乎是同构的。Scala的类与FM中的是一一对应的(首字母缩写),继承关系只包含了一个额外的R和V,通过传递性($\Psi$的自反性和$\Xi$的对称性为了简便而省略了)。
P被声明是sealed,意味着在这个编译单元没有外部的定义了。所以,我们可以枚举所有的Part,得到其中没有一个是vehicles,所以$\text{(P,V)}\in\Xi$。注意如果W或者D不是final的话就不行了,因为扩展这些类可以间接创建新的Part。B和H都是类,并且互相没有继承,所以$\text{(B,H)}\in\Xi$,因为Scala最多只能继承一个类。然而V和H不能从这些定义中得出是否不相交的结论。如果需要这个结论的话,可以通过把V变成sealed或者把H变成final得到。
4.2 空类型
与Scala相比System FM的一个重要的限制是不支持空类型。Scala子类型格的bottom,称为Nothing,提供了一个直接的方式去指代一个值的空集。交集类型同样提供了一种方式构造没有居留元的类型,因为Scala不禁止两个不相交类型的交。空类型在match type的归约时会有问题,因为它打破了一个基础的假设:两个类型不能既是子类型关系又不相交(Lemma3.5)。为了解决这个问题,我们的实现在做归约之前,在scrutinee类型上使用了一个额外的居留性检查。
为了展示为什么空类型会带来问题,我们可以构造一个例子,其中缺少了这个居留性检查,相同的match type可以在两个不同的上下文中归约到不同的结果:
1 | type M[X] = X match { |
这个例子中,在C中的f的定义是type-check的,因为X & String和Int是不相交的(因为String和Int是不相交的),而M[X & String]归约到Int(M的第二个case)。D类通过给出X=Int精化了C的定义。unsoundness自己在D类的体中就体现出来了,其中X & String是Int的一个子类型,而M[X & String]归约到String(M的第一个case)。这样,就可以通过一个string参数调用f,会得到一个运行时错误。而检查scrutinee的居留性可以防止这个错误。在这个例子里,他会防止M[Int & String]做归约,因为Int & String没有居留元。
4.3 空值
在Scala3中,null不再在所有类型中居留了:nullable的类型需要额外的表记,形如A | Null。我们的子类型和不相交性的实现处理了和类型,所以不需要对空值做单独考虑。
4.4 Variance
Scala支持在higher-kinded类型的参数上的variance。这些表记允许程序员特化表记的参数的子类型是如何影响higher-kinded类型的子类型的。例如,type F[+T]定义了一个类型F是它第一个类型参数的协变,意味着如果T1是T2的子类型,那么F[T1]是F[T2]的子类型。反变,写作type G[-T],是相反的意思:如果T1是T2的子类型,那么G[T2]是G[T1]的子类型。
协变和反变的类型似乎总是有相交的,因为对于所有的类型X,都有F[Nothing] <: F[X]和G[Any] <: G[X](其中Nothing和Any是Scala的bottom和top类型)
这段我还没反应过来啥意思,看了后面的例子懂了:
就是实例化两个F[X]、F[Y](或者G[X]、G[Y])的话,就都有F[Nothing] <: F[X]和F[Nothing] <: F[Y],也就是F[Nothing]的居留元也是F[X],F[Y]的,这就相交了。
不过后面讲了,协变的话Nothing作参数的是不会实例化的,所有没有关系。
然而,在协变参数的情况下,当这个类型变量对应着一个field或者构造子的参数的时候,可以做一个例外:Nothing的实例化可以被除外,因为没有任何的运行时程序可以给出一个Nothing类型的值。
这里的实例化大概是
F[Nothing]这个东西,就像Nothing一样可以不考虑了,因为不存在居留元。
比如Scala中的tuple就是这一类的情况。Tuple2是二元组的类,定义如下:
1 | case class Tuple2[+T1, +T2](_1: T1, _2: T2) |
给定两个这个类型的实例化,Tuple2[Int, X]和Tuple2[String, X]。尽管Tuple2[Nothing, X]是它们两个共同的子类型,因为这个类型没有居留元,所以结果是这两个类型还是不相交的。我们的不相交算法实现了这样的推理,得出现有的协变类型参数的不相交性。
4.5 Pattern Matching Exhaustivity
Scala编译器会检查pattern matching的穷尽性来避免由缺少了cases导致的运行时异常。穷尽性通过静态的类继承结构的知识(比如sealed和final表记)来检查在scrutinee类型的每个值是否都被pattern分句包括了。非穷尽的pattern被编译后会附加一个匹配所有情况然后抛出一个运行时异常。System FM使用缺省cases代替系统上的穷尽性检查和运行时异常。
4.6 运行时的类型
Scala的主要平台是Java虚拟机(JVM)。在JVM上,Scala使用偏擦除(patial erasures),即部分的类型保留并翻译到JVM的类型系统,另外部分被擦除,来进行编译。例如,ground class会被直接编译到JVM的类,但类型参数和类型变量会被擦除,并被他们所绑定的东西代替。
擦除直接影响了可以在运行时完成的类型测试。例如,即使case xs: List[Int] =>是一个符合语法的pattern,但这会产生一个编译器警告,因为Int类型参数会被擦除,而不能够在运行时被检查。
这个限制在我们形式化中通过match expression的求值规则和match types的归约规则的区别被反应出来了:求值是限制于静态定义的类(在$\text{E-MATCH2/3}$中的$(C,C_n)\in\Psi$),而match type的归约规则是使用子类型和类型不相交性(在$\text{S-MATCH1/2/3/4}$中的$\Gamma\vdash T_s<:S_n$和$\Gamma\vdash disj(T_s,S_m)$)。
在System FMB中,match expression支持两种参数化pattern:既可以是实例化的(match{xs:List Int},其中$Int\in A$),也可以是用一个绑定pattern变量(match[X]{xs: List X},其中X是pattern variable)。在这个意义上,System FMB比Scala表达力更强,因为实例化的pattern在term level由于类型擦除而不可用了。
4.7 不停机
不同于我们的演算,Scala的实现同样允许match types也递归定义。递归的match types会导致子类型检查无限循环。我们的实现并不检查match types的终止性,因为这样的检查会限制表达能力和便利性。我们通过一个储能机制检查在match type归约时的异常。编译器给定一个初始的能量,每次归约会消耗一个单位。如果编译器没能量了,就停止归约报错“递归超限”。目前的实现是使用一个固定的初始能量值。尽管这看起来对于大部分的实践已经足够,我们还是计划让它可以被设置。这个机制完全是标准的,也已经在很多其他的编程语言中的类型层面的无限递归上使用了。
4.8 类型推断
System FM的类型规则使得任何的match表达式会定型为一个match type,但在完整的Scala语言中不是这样。Scala的pattern matching支持很多种patterns,大多数并没有match type的对应。进一步的,为了保持向下兼容,不能默认把match expression定型成match types。取而代之的是,必须提供一个显式的类型注解。
4.9 缓存
Scala的类型检查算法重度使用缓存来提高性能。而缓存match type归约结果的时候必须采取特别的注意,因为子类型和不相交性检查是上下文相关的。我们的实现对match types使用了一个上下文相关的缓存,可以使得这个结果在新的上下文是自动无效化。朴素的缓存出错的例子见6.4。
4.10 实现的规模
我们的match type的实现对于Scala编译器总的改动大于1500行代码。
5. 案例研究:形状安全的numpy
在这段中,我们通过一个案例研究展示怎么使用match types来表达复杂的类型限制,可以在编译期避免特定的程序错误。为此,我们提供type-level实现的一个多维数组的库的概览,它可以模拟NumPy的API。我们库的目标是提供一个操作n维数组形状安全的接口,其中数组的形状和indice可以被编译期检查,而不是运行时错误。形状和下标的错误在多维数组中是一个广为人知的问题,且已经提出了多个解决方案,尤其是以type-level编程的库的形式出现。我们的库使用的match types提供一个NumPy-like的形状安全的接口。
Scala程序员使用特设的(ad-hoc)方法解决type-level编程问题已经有很长的历史了。这些解决方案有一些缺点,比如编译缓慢,使用也很累赘。Match types旨在简化type-level编程,提供first-class的语言支持。我们相信在这个案例里面展示的这个做法改进了现状,因为它没有使用元编程或者错综复杂的隐式编码来表达type-level的操作。
5.1 Python中的形状错误
在下面的Python代码的例子中,img_batch这个多维数组是25个随机生成的256*256的RGB图片。这个代码是要计算一个长为25的向量来储存这里面每个图片的平均灰度,并且生成一个5*5的图片来表示这个平均灰度的颜色。然而,这个代码存在一个形状错误然后会在运行时出错。
1 | import numpy as np |
这个错误是在np.mean的调用中出现的,它需要一个要做reduce操作的维度的列表作为参数。不幸的是,这个给np.mean的参数都少了一个,结果变成了长度为3(最后一个维度),而不是长度为25(第一个维度);结果就变成了这25张图片的所有RGB分量的均值,而不是25张图片每张的平均灰度了。然后这个reshape操作会在运行时出错,因为它不能把一个3元素的数组转成一个25元素的矩阵。这个错误可能很难定位,因为NumPy的接口reduce维度的时候是基于下标的。想这样的运行时错误如果在很长的计算中出现会带来很大的困扰。
研究了一下numpy里面的维度,就是mean是个array的reduce操作,给定一个维度,它可以把n维的变成n-1维。这里有一个25*256*256的数组,想要reduce成一个长度为25的,那就要是
np.mean(..., (1,2,3)),把后三个维度reduce掉。所以这里的bug刚好差了一个维度。
接下来,我们会展示如何使用match types避免这类的错误。在初步介绍了singleton type(5.2)之后,我们使用HList引入type level的多维数组形状(5.3)。在5.4中,我们展示了np.mean和np.reshape操作基于match types的type-level实现。最后,我们展示了这个新API怎么检查和报出上面这个Python例子的错误的。
5.2 Singleton Types
Scala支持Singleton types,是只有一个值的类型。比如,单例类型1表示包含整数1的类型。Scala标准库包括了几个预定义的match types来表达类型层面的算术计算。例如type +[A <: Int,B <: Int]表示两个整数单例类型的和。在内部,编译器对于这些算术运算时特判使用常量折叠的方式实现的。使用单例类型表示数字在实用性上是需要的,但在这个案例中不是必要的(比如用皮亚诺数字也是可以的)。
5.3 Type-level数组形状
多维数组的形状是一个维度长度的列表;我们说形状$(a_1,a_2,\dots,a_n)$有n维。比如,一个三乘四的矩阵是一个形状是$(3,4)$的二维数组。我们在type level用一个异质类型列表来表示多维数组的形状,称为Shape。我们把这个HList定义成一个有两个构造子的ADT:#:和Ø.
1 | enum Shape { |
原文注:为了清楚起见,我们的表达省略的类型推断所必要的类型边界,比如在Shape类型的定义中
异质列表在Haskell的类型编程里面也介绍过,就是列表的元素的类型可以不同的,而取而代之的是这些类型是编码在列表的类型中的。虽然这里列表里面的值在term level看起来都是Int,但是type level上编码出类型(类似于一个依值类型),它其实每个元素的类型是不同的(不同的singleton type)。
这个类型的定义使我们可以在term level写#:(3, #:(4, Ø)),也可以在type level写#:[3, #:[4, Ø]]。HList类型可以把#:写作中缀形式:3 #: 4 #: Ø。
为了表示n维数组,我们定义NDArray类型。这个类型以多维数组元素类型和多维数组的形状为参数:
1 | trait NDArray[T, S <: Shape] |
我们的目标是在多维数组上定义类型安全的操作,所以我们没有包括值层面上的T和S的定义,但在完整实现中是需要的。
为了构造多维数组,我们定义了random_normal,创建一个给定形状的多维数组,元素为随机的浮点数:
1 | def random_normal[S <: Shape](shape: S): NDArray[Float, S] = ??? |
原文注:这个片段使用了三个问号的操作符,是Scala标准的表示缺失实现的记法。
5.4 用Match Types在形状上做计算
在类型层面编码多维数组的类型和形状使我们可以提供多维数组类型和形状安全的简单操作。例如,元素层面的哈达玛积积,写作np.multiply(x, y),需要数组x和y形状和元素类型都相同。这个限制不需要match types,可以直接表示为:
1 | def multiply[T, S <: Shape](x: NDArray[T, S], y: NDArray[T, S]): NDArray[T, S] = ??? |
然而,对于在数组形状上更复杂的限制,比如reshapes(5.4.1)和reduction(5.4.2)就需要用到match type了。
5.4.1 Reshape
在NumPy中经常用到的一个操作np.reshape,可以改变一个多维数组的形状,但是不改变它里面的值。NumPy API里面的限制是输出的形状的元素数量要和输入的一致。形状的元素数量是所有维度的大小的乘积;比如形状2 #: 3 #: 4 #: Ø就有$2\times 3\times 4=24$个元素。注意形状为Ø的数组是一个标量,所以只有一个元素。这样可以很自然的用match type表达:
1 | type NumElements[X <: Shape] <: Int = |
为了限制reshape只能用于有效的形状,类型系统必须要支持编码一个类型相等的限制。为此,我们利用了Scala的隐式参数,和Scala标准库中的=:=类型相等性限制。
1 | def reshape[T, From <: Shape, To <: Shape](array: NDArray[T, From], newshape: To) |
这个隐式类型参数和我接触过的依值类型编程语言Agda很像,就是像这样type level的一些限制,其实在类型推断的上下文里面都是有的,不用在调用的时候提供,但编译器推断的时候会自动填进去然后检查。这里的ev的类型就是这个限制的一个witness,就很像依值类型里面干的事情了。
使用reshape的这个定义,编译器就会只接受能够证明新旧元素数量相等的那些调用了。这个例子表明了在有单例类型和隐式参数求解下如何使用match types表达强大的限制。
5.4.2 Reduction
NumPy API提供了很多函数在一个维度的集合上对一个多维数组进行reduce,比如np.mean(ndarray, axes)和np.var(ndarray, axes)。axes这个参数是一个维度的列表,列出结果中不再存在的那些维度。维度的列表可以是无序的和重复的,而超界的会产生一个错误。在Python API中,如果传一个None取而代之的话,就会对所有维度都reduce,也就是最后得到一个标量。注意到这与传入一个Ø相反,它表示不reduce任何维度。
这个行为就比之前的例子更复杂了,但仍然可以精确地用match type来表达。我们使用一个match type Reduce,计算这个操作之后的返回的形状。
1 | def mean[T, S <: Shape, A <: Shape](array: NDArray[T, S], axes: A): NDArray[T, |
我们实现给定一个列表的indice的reduction类似于两个嵌套的循环。外层的循环Loop遍历形状并计数当前的下标。内层的循环使用HList上的标准操作Contains和Remove(细节省略)。当Loop到了list的末尾,如果还有要去除的维度,这些就是对于原来的形状超界了:match types故意在这个情况下get stuck。
1 | type Reduce[S <: Shape, Axes <: None | Shape] <: Shape = |
5.5 形状安全
我们定义了random_normal,reshape和mean,就可以在Scala中重写原来Python的例子了:
1 | val img_batch = random_normal(#:(25, #:(256, #:(256, #:(3, Ø))))) |
和预料的一样,对mean的调用会返回一个形状3 #: Ø。因此,reshape的调用不会通过类型检查,因为形状的元素数量是3而不是25。如果我们把错误的地方修改成1 #: 2 #: 3 #: Ø,对reshape的调用就可以通过类型检查,avg_color的形状也是预期中的25 #: Ø。
6. 相关工作
在这一段中,我们重新审视了现有的工作并把match types和dependently typed calculi with subtyping,intensional type analysis,Haskell中的type families和roles和TypeScript中的conditional types做了关联。
6.1 Dependently Typed Calculi with Subtyping
对于把子类型和依值类型结合起来有很多的文献,因此有必要进行全面的调查。相反的,我们提供了我们的阅读之旅的一个浓缩的总结,并解释了是什么让我们决定使用System F<:作为我们形式化的基础。
Dependently Typed Calculi典型地使用同一套语言来描述terms和types。这个归一化在有子类型的情况下同样经常使用。对于term/type有完整对称性的系统来说,这是一个自然的设计,因为这很简练并简化了元理论。遗憾的是,缺少term和type的区别使得这些系统对于我们的目的来说不现实,因为我们的研究是要在一个已有term和type区别的语言上做的。
单例类型在统一和分离的语法之间提供了一个有趣的中间地带,并且在依值类型和子类型的关联中经常被研究。单例类型提供了一种在type中引用term的机制,经常是通过一个类似于集合的语法。这个机制很吸引人,因为它允许类型系统设计者精心挑选可以在类型层面出现的项的构造。当term和type共享很多的构造子的时候,单例类型提供了我们一个清晰的概念。在我们对match types的研究中,对单例类型的最小化使用使得term和type语言共享一个构造子:match的构造子。目前尚不清楚这样做的好处是否会超过额外的复杂性。
Dependent Object Types(DOT)到目前为止Scala类型系统形式化的最重要的工作。DOT 不直接支持任何形式的type-level计算。我们考虑使用 DOT 作为我们工作的起点,除去最近简化 DOT 的soundness证明 ,扩展 DOT 仍然是一个太大的挑战,无法简洁地描述语言扩展。
在多次尝试在现有系统中形式化匹配类型之后,我们决定采用一种更简单的方法,在没有依值类型的系统中添加新的构造。毕竟,System FM 的主要目的是作为一种媒介来简明地解释我们的match types的类型检查算法。出于这个原因,我们将我们的工作建立在 System F<: 之上,我们认为它应该是本节引用的系统中最简单、最熟悉的演算。
6.2 Intensional Type Analysis
在Intensional Type Analysis工作中,Harper and Morrisett引入了$\lambda_i^{ML}$演算支持类型的结构分析。在此之中,类型被表示成可以被“typecase”构造进行case analysis检查的一个表达式,term和type level都支持。Match types可以看成Intensional Type Analysis对于面向对象类继承结构和子类型的一个扩展。$\lambda_i^{ML}$的pattern是受限到一个固定的不相交集合的,而match types需要处理一个开放的类继承关系,而并不是所有的成员都是编译期知道的。这意味着pattern类型可能重叠,我们需要在scrutinee类型和每个pattern类型之间进行一个不相交性分析。不相交性使我们在有重叠pattern和抽象scrutinee类型时可以做安全的归约,同时保留了模式匹配的自然的顺序求值的顺序。
6.3 Haskell的类型家族
Haskell的类型家族允许程序员可以使用模式匹配定义type-level的函数。默认情况下,类型家族是open的,意味着一个定义可以在多个文件和编译中蔓延。这个灵活性给类型家族带来了一个严格的限制:pattern不能重叠。这个限制的一个好处是它防止了类型家族做归约时候的二义性(pattern两两不相交),这对于分开的定义来说是必需的。Open的类型家族非常适合和类型类结合,因为这两个构造都是由不相交限制而开放定义的。
Closed的类型家族(CTFs)允许类型家族的重叠定义。不像open的变种,CTF的归约是顺序的,基于归一化和apartness检查。这样看来,CTFs和match types就很像了。事实上,如果我们把unification检查换成subtyping,把apartness检查换成不相交性,他们的归约算法和我们的完全一致,从一个高阶的角度来看的话。
默认情况下,Haskell会检查递归类型家族的停机性,但是这个检查也可以关掉来提高类型家族的表达能力。尽管目前的形式化没有包括不终止的类型家族,这个论文讨论了不停机性带来的soundness问题。这个问题只在pattern中存在重复类型绑定时出现。在Scala中,match types(和广义的模式匹配)不允许重复的绑定,所以不受这个问题的影响。
6.4 Haskell中的类型角色
Haskell中引入类型角色来解决一个持续了很长时间的,有open类型家族和newtype构造结合带来的unsoundness问题。我们理解类型角色是一个类型的注解来指定一个类型是否可以安全地名义上的和其他类型比较,还是说应该使用representational equality(RE) 。在RE中的representation是指一个类型在运行时的表示。具体来说,RE是newtype别名的析构。
如果没有类型角色的话,类型家族的归约会有unsoundness。这个例子翻译成Scala是这样的:
1 | trait AgeClass { |
在这个例子中,Age在AgeClass里面是抽象的,在AgeObject里是具体的。在Haskell没有类型角色的情况下,如果这个例子和一个区分Int和Age的类型家族结合就会unsound。这样的类型家族在AgeClass中会reduce得不一样,因为类型不一样,而在AgeObject中因为两个类型是同义,所以会得到一个运行时错误。
幸运的是我们的match types没有这个问题。因为子类型(和不相交性)会保护我们的实现防止在Age是抽象的时候错误的区分Int和Age。考虑下面的match type(直接翻译自Haskell出错的例子):
1 | type M[X] = X match { |
我们的算法在AgeClass不会把M[Int]reduce到Bool,因为这个归约需要提供Age和Int不相交,但是当Age是抽象类型的时候这个无法做到。
6.5 TypeScript的Conditional Types
TypeScript的conditional types是一个基于子类型的type-level三目运算符。Conditional types可以嵌套在pattern的序列中,让它可以和match types类似。
TypeScript语言specification简要地介绍了有类型变量时的归约conditional types的算法。给定一个类型S extends T ? Tt : Tf, TypeScript编译器首先将S和T中的类型参数换成any(TypeScript子类型格的top)。如果替换的结果类型不是子类型关系,那么整个condition归约到Tf。不幸的是,这个算法既unsound又incomplete。
Unsoundness是因为在反变的地方错误的拓宽了类型变量。尽管TypeScript不提供variance的标注,但函数类型对于返回类型是协变的,对于参数类型是反变的。Conditional type的unification算法错误近似了X => string到any => string,把前者合一到后者,会导致一个运行时错误。
Incompleteness是因为类型参数的近似不能作为类型参数的边界。考虑下面的例子:
1 | type M<X> = X extends string ? A : B |
这里,TypeScript的归约算法不能识别new A可以被定型为M<X>,尽管X显然是f体中的string的一个子类型。
尽管情况令人担忧,但考虑到稳健性不是 TypeScript 类型系统的目标,它可能并没有看起来那么糟糕。尽管如此,我们相信这篇论文的结果直接适用于条件类型,可以用来改进 TypeScript 的类型检查器。
7. 结论
In this paper, we introduced match types, a lightweight mechanism for type-level programming
that integrates seamlessly in subtyping-based programming languages. We formalized match types
in System FM, a calculus based on System F<:, and proved it sound. Furthermore, we implemented
match types in the Scala 3 compiler, making them readily available to a large audience of pro-
grammers. A key insight for sound match types is the notion of disjointness, which complements
subtyping in the match type reduction algorithm. In the future, we plan to investigate inference of
match types to avoid code duplication in programs that operate both at the term and the type level.
- 本文作者: Frankenstein
- 本文链接: https://salty-frankenstein.github.io/blog/2022/03/01/【PL】Type-Level-Programming-with-Match-Types/
-
版权声明:
 本博客文章采用 CC BY-SA 4.0 协议进行许可。转载请注明作者与原文链接。
本博客文章采用 CC BY-SA 4.0 协议进行许可。转载请注明作者与原文链接。