2019-07-24

【小课堂】八、算法初步

至此，小课堂基础篇的语法部分就告一段落了，我们已经学习了最常用的C/C++语言语法；从哲学的角度说，现在我们已经可以使用C/C++语言的这些语句实现计算机能做的一切功能了。然而在现实的编程操作过程中却并不这么理想，好像经常会出现有一个需求却不知道如何实现的情况（如果你在之前的课程中打星号的习题上遇到过困难的话）；这就是我们学习算法的目的。
在这一节，我们将了解什么是算法，了解一些常用的基础算法以及实现，并初步学习计算算法复杂度的方法。

什么是算法

算法就是解决问题的一系列流程。
算法的概念始终伴随着我们的数学学习过程（只是时不时地被淡化了），现在回忆小时候学用竖式计算多位数加法的过程：从低位开始，按位相加，超过10了要进位，进位要参与下一位的运算中，直到算到某数到头了，另一个数剩余部分抄下来，算法结束。
这个看似简单的算法，却有着大用处——这就是高精度计算。
请看下例：
例8.1
输入两个正整数a,b（a,b<$10^{500}$），输出a+b的值

我们发现，在C/C++语言中数的大小受到限制，而假如我们要用C/C++语言进行上百甚至上千位的计算，使用内置的int（long long也不行）就无能为力了。而此时，使用竖式加法的算法就能解决这个问题：

使用字符串读取两个大整数
使用竖式加法算法进行计算，结果储存在另一个字符串中
输出结果字符串

于是，我们就可以这么写：

//高精度加法算法
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
char s1[1000],s2[1000],ans[1000];

void add(){
    if(s1[0]=='0'&&s2[0]=='0'){
        strcpy(ans,"0");
        return;
    }
    
    int al=strlen(s1),bl=strlen(s2);
    int a[1000]={0},b[1000]={0},c[1000]={0};
    int i,j,jw=0,t1,t2=0;
    
    for(i=0;i<al;i++)
        a[i]=s1[al-1-i]-'0';
    
    for(i=0;i<bl;i++)
        b[i]=s2[bl-1-i]-'0';
    
    t1=max(al,bl);
    for(i=0;i<t1;i++){
        c[i]=a[i]+b[i]+jw;
        jw=c[i]/10;
        c[i]%=10;
    }
    
    c[i]=jw;
    while(c[i]==0)i--;
    for(;i>=0;i--){
        ans[t2]=c[i]+'0';
        t2++;
    }
    ans[t2]='\0';
}

int main(){
    scanf("%s%s",s1,s2);
    add();
    puts(ans);
    return 0;
}

复杂度

在设计出一个好的算法之前，首先要思考如何评判一个好的算法。在使用计算机的过程中，我们知道完成一个相同的任务，如果一个软件占用更小的内存，需要更少的运行时间（意味着更流畅的用户体验），那么它是更优的。这里引入空间复杂度和时间复杂度的概念。
由于复杂度的概念有确切的数学定义，对于给定算法也有严格的复杂度计算、证明方法；这里只是做初步介绍。
这里的空间就是内存空间的占用，而时间则是运算量对运行时间的占用。然而要注意，所谓复杂度并非指程序一次运行过程中占用空间或时间的多少，而是空间、时间的占用随输入规模的变化快慢。
如何计算时间复杂度？
我们可以将程序的语句执行次数可以用一个与输入有关的代数式表示，取这个代数式的最高次项且忽略此项系数作为时间复杂度。
例：

1
2
3

//A
for(int i=1;i<=5;i++)
    cout<<i<<endl;

程序A中的cout语句执行了$5$次，与输入无关，为一个常数（也可以说最高次项是零次项），我们称这段程序的时间复杂度为$O(1)$，常数时间复杂度。

//B
int n;
cin>>n;
for(int i=1;i<=n;i++)
    cout<<i<<endl;

程序B中的cin语句执行了1次，cout语句执行了$n$次，与输入n有关，运算次数是$n+1$（最高次项是n的一次项），我们称这段程序的时间复杂度为$O(n)$，线性级时间复杂度。

//C
int n;
cin>>n;
for(int i=1;i<=2*n;i++)
    for(int j=1;j<=n;j++)
        cout<<i<<" "<<j<<endl;
for(int i=1;i<=n;i++)
    cout<<i<<endl;

程序C中的cin语句执行了1次，第一个循环cout语句执行了 $ 2*n*n $ 次，第二个循环cout语句执行了 $n$ 次，运算次数是$2n^2+n+1$（最高次项是n的二次项），我们称这段程序的时间复杂度为 $O(n^2)$ ，平方级时间复杂度。

如此定义时间复杂度的原因是：许多算法往往在输入较小的情况下都差不多（都是瞬间解决），而随着输入增大，运算需要的时间也会增加，但此时不同复杂度的算法增长快慢也不同。一个好的算法在数据量很大的情况下依然有好的表现。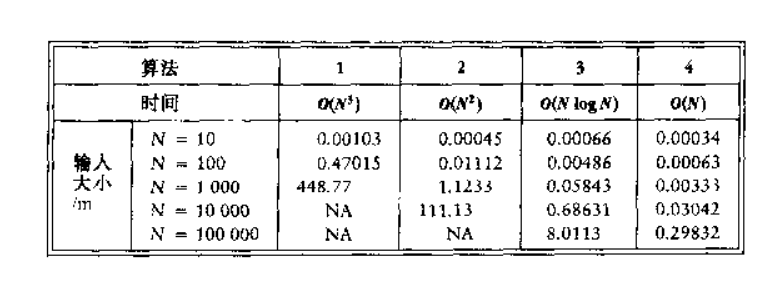

图8.1，摘自《数据结构与算法分析：C语言描述》
下面将以排序算法为例体验不同算法复杂度的不同，并介绍算法复杂度计算方法。

排序算法

在之前学习分支、循环、数组的时候，都做过关于排序的题；而在高一信息课上也曾学过冒泡排序算法。原因一是因为它是个很好的例子；二是排序确实是个重要的算法——试想如果一本词典不按字典序，而是随机编写，那么我们每次查询都要从头翻起。排序是快速查找的基础。

引入

那么如何得到一个有序的序列（排序）呢？比如，给定一个长度为n的数组，要求从小到大排序。我们先想简单一些：我们先找最小的，放第一个；然后找第二小的，放第二个……这样找n次，就得到了一个从小到大的序列：

#include<iostream>
#include<cstdio>
using namespace std;

int main(){
    int n;
    int a[1000],b[1000];
    bool visited[1000]={0};     //标记是否取过
    int m,position;             //记录最小值
    int infinity=2147483647;    //这是最大的可能值（int类型的上限）
    
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]); 
    
    for(int i=1;i<=n;i++){      //找n遍
        m=infinity;
        for(int j=1;j<=n;j++)   //从头找到尾
            if(a[j]<m && !visited[j]){//a[j]如果比当下的最小值还小，且没取过
                m=a[j];         //新的最小值
                position=j;     //记录位置
            }
        b[i]=m;                 //放入第i个最小值 
        visited[position]=1;    //标记 
    }
    
    for(int i=1;i<=n;i++)
        printf("%d ",b[i]); 
    
    return 0;
}

花了些工夫，也实现了这个功能，看上去就很复杂——看来想起来简单的算法未必是最好的。了解了复杂度的概念后，我们可以从时间复杂度和空间复杂度两个角度评判这个算法，再想办法加以改进。

时间复杂度：
不计输入输出，排序部分循环执行$n*n$次，时间复杂度为$O(n^2)$
空间复杂度：
不计原始数组，排序部分共使用了一个长度为n的整型数组b，和长度为n的布尔型数组visited，空间复杂度为$O(n)$

选择排序

如果我们从空间方面考虑优化，就会发现找到最小值之后不一定要放在另一个数组b中，而可以直接在原数组a中改变顺序：找到最小值后与原a[1]交换，找到第二小值后与原a[2]交换……最终有序序列存放在a中，上面的b数组和visited数组就节省掉了。
于是我们得到了以下经过优化的代码：

#include<iostream>
#include<cstdio>
using namespace std;

int main(){
    int n;
    int a[1000];
    int m,position,t;             //记录最小值
    int infinity=2147483647;    //这是最大的可能值（int类型的上限）
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]); 
    
    for(int i=1;i<=n;i++){      //找n遍
        m=infinity;
        for(int j=i;j<=n;j++)   //在剩余的元素中找 
            if(m>a[j]){
                m=a[j];
                position=j;
            }
        t=a[i];                 //放入a[i]的位置（交换） 
        a[i]=a[position];
        a[position]=t;
    }
    
    for(int i=1;i<=n;i++)
        printf("%d ",a[i]); 
    
    return 0;
}

时间复杂度：
不计输入输出，排序部分循环执行 $\frac{1}{2}*n*n$ 次，时间复杂度仍为$O(n^2)$（常数比之前的稍小，但仍是同一级别）
空间复杂度：
不计原始数组，排序部分只使用了几个临时变量，空间复杂度为常数$O(1)$

经过上述优化的这种排序算法学名为选择排序。正如上面分析的，选择排序的时间复杂度为$O(n^2)$，空间复杂度为$O(1)$。

*更进一步的优化

上述选择排序的时间复杂度$O(n^2)$仍然可以进一步优化：内层循环$O(n)$的寻找最小值操作可以借助一种叫堆的数据结构将复杂度降低至$O(logn)$，从而使整体复杂度降为$O(nlogn)$。这种排序算法名为堆排序，然而由于涉及数据结构的知识，这里不详细介绍，如感兴趣可自行搜索。

这里介绍一种时间复杂度同样是$O(nlogn)$的算法，归并排序。

*归并排序

我们先引入一种将两个有序序列合并成一个有序序列的算法：二路归并。

#include<iostream>
#include<cstdio>
using namespace std;

int main(){
    int a[10]={1,2,5,6,7,8};        //有序数组a，共6个元素 
    int b[10]={2,3,6,7,9,12,13};    //有序数组b ，共7个元素 
    int t[20];                      //合并的新数组 
    int pa=0,pb=0,k=0;              //a,b,t数组的当前位置，初始为0 
    while(pa<6 && pb<7)             //a,b数组都没到末尾，则循环 
        if(a[pa]<b[pb]){            //如果当前是a的元素小
            t[k]=a[pa];             //则t中放入a的当前元素 
            pa++;                   //指向a的下一个元素 
            k++;                    //指向t的下一个空位 
        }
        else{                       //否则是b的元素小 
            t[k]=b[pb];
            pb++;
            k++;
        }
        
    while(pa<6){                    //如果a数组还没到末尾 
        t[k]=a[pa];                 //将a的元素接在t数组末尾 
        pa++;
        k++;
    }
    
    while(pb<7){                    //否则将b数组接在t的末尾 
        t[k]=b[pb];                 //注意这两个循环不会都执行 
        pb++;
        k++;
    }
    
    for(int i=0;i<13;i++)           //输出结果：1 2 2 3 5 6 6 7 7 8 9 12 13 
        printf("%d ",t[i]);
    
    return 0;
}

这个算法总共只将a,b两个数组从头扫描至末尾，如果两个序列长度分别为$m,n$，则二路归并的时间复杂度为$O(m+n)$

归并排序就是借助二路归并和递归思想实现的排序算法：
先将排序序列平分成左右两个部分：

如果排序的序列的两个部分都是有序序列，那么我们可以用二路归并排成有序，排序完成。
如果排序的序列左右两个部分不是有序序列，那么就继续平分成两个部分进行归并排序（递归）
如果分割到只剩一个元素了，那左右两部分就一定是有序的，直接归并（递归的基本条件）

于是，归并排序就可以这样实现：

#include<iostream>
#include<cstdio>
using namespace std;
int a[1000],t[1000];

void mergesort(int l,int r){    //两个参数分别为排序的左右边界
    if(l==r)return;             //区间只有一个元素 
    int mid=(l+r)/2;            //中间位置下标 
    mergesort(l,mid);           //递归排序左半边 
    mergesort(mid+1,r);         //递归排序右半边 

    int i=l,j=mid+1,k=l;        //递归结束，此时左右两序列已经有序 
                                //下面将两部分进行二路归并 
    while(i<=mid&&j<=r)
        if(a[i]<a[j]){
            t[k]=a[i];i++;k++;
        }
        else{
            t[k]=a[j];j++;k++;
        }

    while(i<=mid){
        t[k]=a[i];k++;i++;
    }
    while(j<=r){
        t[k]=a[j];k++;j++;
    }

    for(i=l;i<=r;i++)
        a[i]=t[i];
}

int main(){
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]); 
    
    mergesort(1,n);
    
    for(int i=1;i<=n;i++)
        printf("%d ",a[i]); 
    return 0;
}

对于一个长度为$n$的数组，每次二分区间直到单元素，一共是$logn$次（在信息学中，$log$默认的底数为2）；而上面分析二路归并的复杂度为$O(n)$级，因此，归并排序的时间复杂度为$O(nlogn)$，是一种高效的排序算法。
从归并排序一例中，我们也认识到递归的真正威力。

*搜索算法初步

计算机的最大优势就是快速的运算能力，我们可以利用这点进行人工无法实现的大量重复劳动。然而要达到这一要求也需要算法的支持，这就是搜索算法。

深度优先搜索

例8.2
有A~E五人，和1~5五本书，每个人对每本书各有喜好（如下表所示），找出所有让每个人满意的发书方案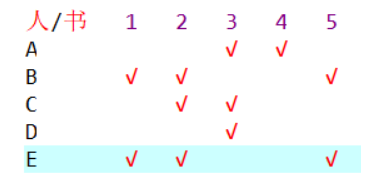

这题的思路很简单，把所有发书情况（$P^5_5$）全部枚举，判断是否符合要求，输出符合要求的方法。然而，怎么让计算机枚举这些情况呢？
我们首先使用一个二维数组like表示上面的表格，like[i][j]就表示第i个人是否喜欢第j本书（下标从1开始）：

bool like[10][10]={ {0,0,0,0,0,0},
                    {0,0,0,1,1,0},
                    {0,1,1,0,0,1},
                    {0,0,1,1,0,0},
                    {0,0,0,0,1,0},
                    {0,1,1,0,0,1}};

然后就是枚举了。这里引入深度优先搜索（dfs）算法解决这一问题。
我们先定义数组a，a[i]表示第i个人发到的书的编号，如a[2]=5表示第二个人发到第五本书。然后我们就可以试着按照要求填写这一数组，当a[1]到a[5]全部填满时就是满足条件的一组解了。

int a[10];//记录结果
bool b[10];//记录书的发放情况
void book(int i){//参数表示当前发到第i个人
    int j;
    for(j=1;j<=5;j++)//枚举五本书
        if(!b[j]&&like[i][j]){//如果第j本书没有发放，并且第i人喜欢第j本书
            a[i]=j;//发书：将第i个人的书标记为第j本
            b[j]=1;//标记第j本书已经发出
            if(i==5)write();//如果到了第五个人，说明五本书都已经成功发放，就输出
            else book(i+1);//发下一个人的书
            b[j]=0;//此时在i发第j本情况下，第i+1个人的情况已枚举完毕，于是解除第j本的标记，准备开始发第j+1本
        }
}

现在请用纸笔模拟一遍上述代码的运行过程和输出。

我们可以发现，深度优先搜索的过程就是利用了搜索时每一个阶段的相似性进行递归求解；而求解过程符合思考时的逻辑，先 深度优先 地寻找到一组解，找完一组解后当前递归的结束，回退以寻找下一组解，这样可以很好的检验每一组解，保证解的正确性；最后的运行次数也就是本题的枚举次数：$5!$次，保证不重不漏。

由此我们可以得到深度优先搜索的一般形式：

void dfs(int i){
    int j;
    for(j=1;j<=maxj;j++)
        if(新节点符合条件){
            记录新节点;
            if(到目标节点)输出;
            else dfs(i+1);
            删除节点;
        }
}

其中记录节点与删除节点的语句应为逆运算关系，保证回到原先状态，进行下一次搜索。
需要注意的是，深度优先搜索算法的时间复杂度是指数级的，取决于你需要枚举的种类数，可以发现上例中五个人五本书$n=5$如果换成$n=100$，枚举种数将是天文数字，也就不能使用搜索算法求解了。

搜索算法补充阅读（友情链接）：比较深奥

作业

思考

1、什么是算法？为什么要学习算法？算法和代码的关系是什么？
2、什么是算法复杂度？如何计算时间/空间复杂度？复杂度这一概念有什么作用？
3、既然排序算法的功能都完全一致，为什么还要发明那么多种不同的排序算法？

习题

1、输入两个正整数a,b（a,b<$10^{500}$），输出a-b的值，并分析你的算法的复杂度
*2、输入两个正整数a,b（a,b<$10^{500}$），输出a*b的值，并分析你的算法的复杂度
**3、快速排序是也是一种高效的排序算法。与归并排序类似，快速排序算法也是使用了分治和递归的思想，其中一种描述如下：

取序列的正中间元素作为标准，将序列分成两部分，将比标准小的元素放在标准左边，大的元素放在右边
对左右两部分也分别进行快速排序（递归）
直到分割成单元素（递归的基本条件）

也可以看看这个视频帮助理解
请按照描述（可仿照归并排序）实现快速排序算法，并分析其复杂度
**4、八皇后问题为：国际象棋棋盘上放置8个互相不能攻击到的皇后的摆法有多少种？（国际象棋棋盘为8*8，皇后可以攻击到同行、列与两条对角线的棋子），使用深度优先搜索算法求解八皇后问题

提示：可以使用以下方法传递数组为函数的参数，不同于普通参数的传值，数组作为参数传递的是数组自身。这意味着函数中对传入的数组进行操作将改变这个数组

#include<iostream>
using namespace std;

void ArrayProcedure(int a[]){
    a[0]=10;
}

int main(){
    int t[10];
    for(int i=0;i<10;i++)
        t[i]=i;
    
    ArrayProcedure(t);
    
    for(int i=0;i<10;i++)
        cout<<t[i]<<endl;
    return 0;
}

输出：
10
1
2
3
4
5
6
7
8
9

地灵殿旧址

你确定要看？