小课堂

【小课堂】五、函数（2）

声明与定义

由于作用域是从声明开始的，所以在声明之前，一个名字是无法被使用的：

1
2
3
4
5
6
7
8
9
int f1(){
    //此处全局a未声明，不在作用域内，无法使用
}

int a;//声明全局量a

int f2(){
    //此处全局a已声明，在作用域内，可使用
}

与之类似的，一个函数也有作用域，一个函数名也只在它被声明之后才能使用： 

1
2
3
4
5
6
7
8
9
10
11
int f1(){
    //此处函数a未声明，不在作用域内，无法调用
}

int a(){
    ……
}

int f2(){
    //此处函数a已声明，在作用域内，可调用
}

那么，如果函数f1中也需要调用函数a该怎么处理呢？显然，一种办法是更改声明顺序： 

1
2
3
4
5
6
7
8
9
10
11
12
int a(){
    ……
}

int f1(){
    //此处函数a已声明，在作用域内，可调用
}


int f2(){
    //此处函数a已声明，在作用域内，可调用
}

而这里介绍另一种方法解决这一问题，我们引入一组之前一直混用的概念：声明（declaration）和定义（definition） 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int a();//声明函数a

int f1(){
    //此处函数a已声明，在作用域内，可调用
}

int a(){//定义函数a
    ……
}

int f2(){
    //此处函数a已声明，在作用域内，可调用
}

声明：我们让函数a先提前出现，扩大了定义域，但并不需给出具体的函数实现（需要有除函数体外的其它部分）
定义：真正实现函数a的功能，需要完整的函数信息（包括函数体）
须注意，一个函数在代码中可以声明任意次，但只能定义一次；而声明过的函数如果没有完整定义也无法调用。

类似的，对于变量其实也存在声明与定义之分（有时须借助extern关键字，这句话可跳过）： 

1
2
3
4
int a;//声明变量a
int b = 4;//定义变量b，赋初值为4
int m[100];//声明数组m
int n[100]={0};//定义数组n，并初始化

其中的区别是：声明只是告诉编译器这个变量的出现，而定义则会为这个变量分配内存，此区别在使用数组时会更为明显——如果只是声明一个变量，却一直没有使用的话，在程序运行的过程中是不会消耗内存的。
虽然因为C/C++语言中写法区别不大，也是一些（不合格）程序员都容易混淆的概念，但确实是很有必要区分的；而在之后学习递归时会遇到的互调递归则更离不开声明、定义分离的写法。

递归（1）

从前有座山，山上有座庙，庙里有个老和尚给小和尚讲故事，讲的是：从前有座山，山上有座庙，庙里有个老和尚给小和尚讲故事，讲的是：……
这段著名的神秘小故事，最迷人的部分就在于：老和尚讲的故事，就是它这个故事本身。
这种自我指涉的现象随处可见：树枝的分叉上还是分叉、分形曲线、汉诺塔……
类似地，C/C++的函数可以调用自身，我们把函数调用自身的操作称为递归，把调用了自身的函数称为递归函数。
然而，正如 老和尚的故事 一样，如果调用自身不加限制，便会无穷无尽循环下去（然而计算机空间并非无限，于是程序就会崩溃）。因此，递归也必须加以限制。

考察以下阶乘定义：
$n! = n ×(n-1)!,n>0$
$0! = 1$
第一行定义n的阶乘等于n乘以n-1的阶乘。发现在阶乘的定义中出现了阶乘本身，我们称阶乘是递归定义的。然而，n-1的阶乘又是多少呢？是n-1乘以n-2的阶乘……如果不加以控制，就必然会坠入负无穷，重演老和尚的悲剧。
因此，第二行，定义0的阶乘为1，这是其它所有自然数递归的终点，我们称之为递归的基本条件。
这样一来，所有自然数的阶乘都有了明确定义。我们可以以此为依据编写阶乘函数的另一种写法（第一种见例5.1）： 

1
2
3
4
int factorial(int n){
    if(n==0)return 1;//递归的基本条件
    else return n * factorial(n-1);//递归求解
}

对应上面的定义，发现代码的写法是完全一致的。但是在调用这个阶乘函数时，计算机内又发生了什么呢？（以下为重点，前方高能，请反复观察）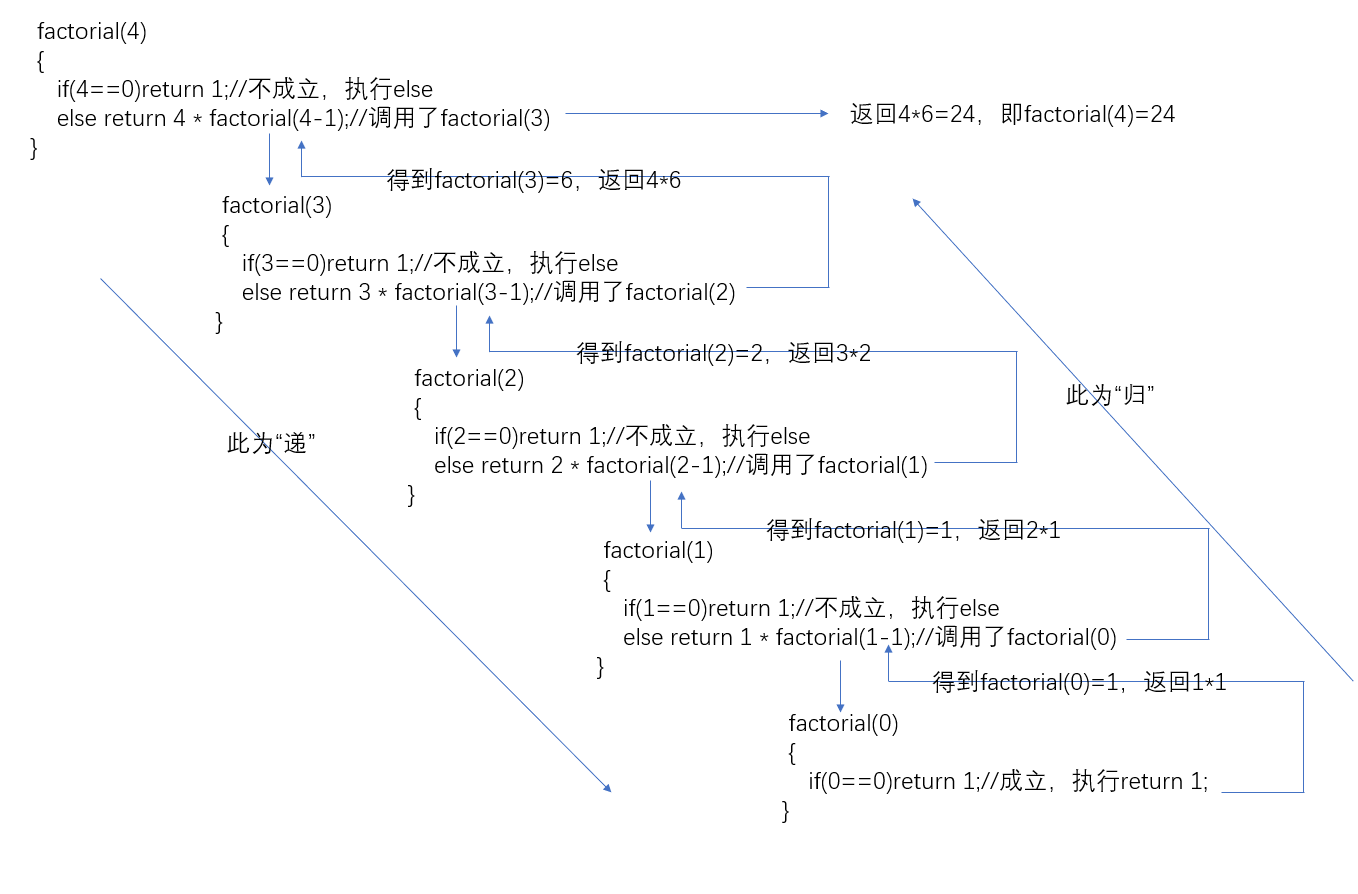
97015ab86aa887ce87b698d9011c78f0.png
现在请反复观察这张深度好图（）
我们发现计算机执行方法和普通函数并无不同，遇到调用自身则视为调用了另一个函数（新建了另一个局部量n，原n不变），一直调用到factorial(0)，此时共有5个局部量n，值分别为4,3,2,1,0。到factorial(0)执行return语句，也是将值1代回到调用它的地方factorial(1)的return语句中，然后factorial(1)执行return语句……直到回到factorial(4)，计算得出factorial(4)=24，递归调用结束。

递归是初学时相当难掌握的概念，极可能会出现一头雾水或自以为理解却并非正确的情况发生。我们现在需要先充分理解上面的阶乘一例，接下来再分析更多的递归程序进行归纳，之后再通过作业习题进行训练检验。毕竟，递归概念极其重要，是将来程序设计中不可避免使用的技术，也是衡量程序设计水平高下的重要标尺之一。
我们对递归这一节的要求是：

  • 理解什么是递归
  • 能读懂一段递归代码的含义
  • 能分析出一个递归函数在计算机内部的执行过程
  • 能正确计算出给定递归函数的返回值
  • 能编写递归函数正确实现某一功能，不出现故障（bug）

下面继续我们的探险：

递归（2）

还有一种形式的递归： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int a();
int b();

int a(){
    ……
    b();
}

int b(){
    ……
    a();
}


注：此处的递归的基本条件未补全
这种函数自身未调用自身，但调用了调用自身的函数，也是一种特殊的递归，称为互调递归；由于C/C++作用域限制，需要先进行声明，先定义的函数才能调用后定义的函数。
下面是一个例子： 

1
2
3
4
5
6
7
8
9
10
11
12
bool odd(int n);

bool even(int n){
    if(n==0)return true;
    else return odd(n-1);
}

bool odd(int n){
    if(n==0)return false;
    else return even(n-1);
}

even函数返回整数n是否为偶数，odd函数返回整数n是否为奇数。利用n与n-1奇偶性相反进行递推，0为偶数作为基本条件，即可实现。

对递归函数效率的思考

考察以下斐波那契数列定义：
注：$fib(n)$表示斐波那契数列的第n项
$fib(n) = fib(n-1) + fib(n-2), n>2$
$fib(1)=fib(2)=1$
fib的定义同样用到了自身，所以它也是递归定义的。因此我们也可以用递归的方法计算。 

1
2
3
4
int fib(int n){
    if(n==1 || n==2)return 1;
    else return fib(n-1) + fib(n-2);
}

现在布置第一个任务：仿照上面分析阶乘函数图片的形式，试着分析调用函数fib(5)时的计算过程。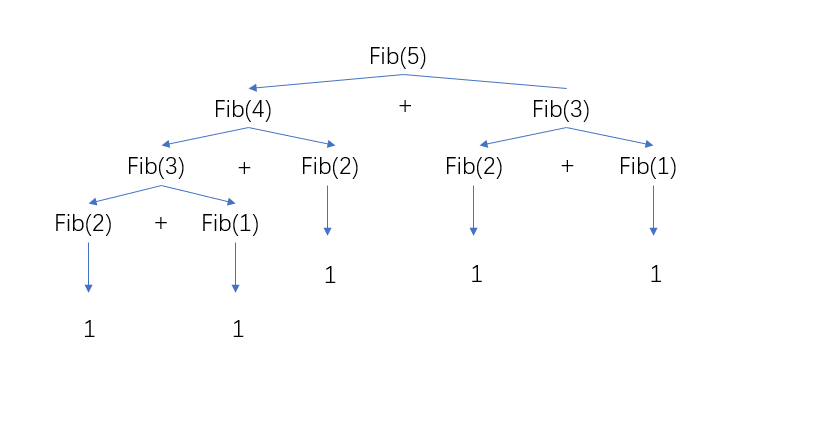
fib.png
我们发现，计算fib(5)时调用了fib(4)和fib(3)；计算fib(4)时调用了fib(3)和fib(2)；计算fib(3)时调用了fib(2)和fib(1)；其中fib(3)被计算了2次，在fib(4)的左侧和fib(5)的右侧，fib(3)被反复计算。而随着n的增大，这张树形图将迅速增大。现在请尝试让你的计算机计算fib(45)的值，记录运算时间，并与之前你编写的循环结构求解斐波那契数列第45项的程序进行对比。（你想尝试更大的数可能要等很久很久）
循环结构求解斐波那契数列只执行45次，是瞬间即可得出结果；而递归求解却花了5秒（仔细观察发现递归求解斐波那契数列就是一个个1加出来的，运算量等于fib(n)，之后会知道此算法复杂度$O(2^n)$ ，为指数级），运算量差了许多数量级。
究其原因就是上面说的重复计算（称为冗余计算）大大浪费了算力；在递归求斐波那契数列的算法时出现的反复计算被称为重叠子问题。因此，在编写递归函数时，估算它的运算量也是必要的一个环节，而像上面的存在重叠子问题的递归算法则一定要警惕，并想办法优化，下面提供一种可行的优化方法供参考（此方法是解决递归时重复计算的常规方法：记忆化）： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include<iostream>
using namespace std;
int f[1005]={0,1,1};
int fib(int n){
    if(f[n]!=0)return f[n];
    else{
        f[n]= fib(n-1) + fib(n-2);
        return f[n];
    }
}

int main(){
    cout<<fib(45)<<endl;
    return 0;
}

此程序将递归过程中已经计算过的结果保存在f数组中（记忆化），重复调用时将直接返回结果，避免了重复计算，运算量也大大降低了。

作业

思考

1、什么是声明？什么是定义？C/C++中为什么要区分这两者？
2、什么是递归？这种写法的好处是什么？可能的坏处是什么？
3、如何计算调用一个递归函数的执行次数？（即复杂度）

习题

1、

1
2
3
4
5
6
int func(int n){
    if(n==1)return 1;
    if(n==2)return 2;
    return func(n-2)-func(n-1);
}
//pj2014T2

计算func(7)的值（不使用计算机）

*2、

1
2
3
4
5
6
7
int r(int n){
    if(n<=5)return n;
    for(int i=1;i<=5;i++)
        if(r(n-i)<0)return i;
    return -1;
}
//tg2010T3

计算r(16)的值（不使用计算机）
3、编程计算$Ackermann$函数$(m≤3)$，其中：
$Ackermann(m,n)=$
    $n+1,(m=0)$
    $Ackermann(m-1,n+1),(n=0)$
    $Ackermann(m-1,Ackermann(m,n-1)),(m,n≠0)$
4、编写一个递归函数，传入一个正整数参数n，返回数列$a_n=2n+1$的前n项和
*5、编写一个递归过程，转入一个正整数参数、倒序输出其各数位的数字
要求主函数： 

1
2
3
4
5
6
int main(){
    int n;
    cin>>n;
    func(n);
    return 0;
}

输入：
123456
输出：
654321
**6、编写一个递归过程，传入一个正整数参数、输出其二进制形式